设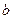 和
和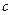 分别是从1,2,3,4这四个数中随机选取的数,用随机变量X表示方程
分别是从1,2,3,4这四个数中随机选取的数,用随机变量X表示方程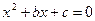 的实根的个数(重根按一个计)。
的实根的个数(重根按一个计)。
(1)求方程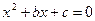 有实根的概率;(2)求随机变量X的分布列和数学期望;
有实根的概率;(2)求随机变量X的分布列和数学期望;
(3)若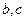 中至少有一个为3,求方程
中至少有一个为3,求方程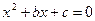 有实根的概率。
有实根的概率。
推荐套卷
设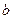 和
和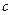 分别是从1,2,3,4这四个数中随机选取的数,用随机变量X表示方程
分别是从1,2,3,4这四个数中随机选取的数,用随机变量X表示方程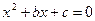 的实根的个数(重根按一个计)。
的实根的个数(重根按一个计)。
(1)求方程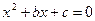 有实根的概率;(2)求随机变量X的分布列和数学期望;
有实根的概率;(2)求随机变量X的分布列和数学期望;
(3)若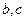 中至少有一个为3,求方程
中至少有一个为3,求方程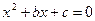 有实根的概率。
有实根的概率。