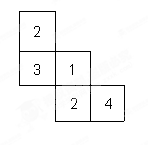
如图,在平面直角坐标系中,点A的坐标为(1,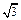 ) ,点B在x轴的负半轴上,
) ,点B在x轴的负半轴上,
∠ABO=30°.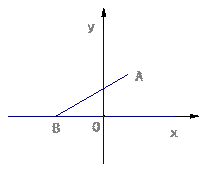
(1)求过点A、O、B的抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点C,使AC+OC的值最小?若存在,求出点C的坐标;若不存在,请说明理由;
(3)在(1)中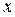 轴下方的抛物线上是否存在一点P,过点P作
轴下方的抛物线上是否存在一点P,过点P作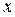 轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3 ?若存在,求出点P的坐标;若不存在,请说明理由.
轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3 ?若存在,求出点P的坐标;若不存在,请说明理由.
相关知识点
推荐套卷
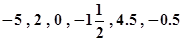 ,
, ,-(-1),并将它们的相反数用“<”符号连接起来.
,-(-1),并将它们的相反数用“<”符号连接起来. )-[(-4
)-[(-4 )]+ |-8+3|
)]+ |-8+3| 粤公网安备 44130202000953号
粤公网安备 44130202000953号