近期世界各国军事演习频繁,某国一次军事演习中,空军同时出动了甲、乙、丙三架不同型号的战斗机对一目标进行轰炸,已知甲击中目标的概率是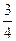 ;甲、丙同时轰炸一次,目标未被击中的概率是
;甲、丙同时轰炸一次,目标未被击中的概率是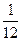 ;乙、丙同时轰炸一次都击中目标的概率是
;乙、丙同时轰炸一次都击中目标的概率是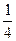 。
。
(Ⅰ)求乙、丙各自击中目标的概率。
(Ⅱ)求目标被击中的概率。
推荐套卷
近期世界各国军事演习频繁,某国一次军事演习中,空军同时出动了甲、乙、丙三架不同型号的战斗机对一目标进行轰炸,已知甲击中目标的概率是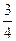 ;甲、丙同时轰炸一次,目标未被击中的概率是
;甲、丙同时轰炸一次,目标未被击中的概率是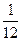 ;乙、丙同时轰炸一次都击中目标的概率是
;乙、丙同时轰炸一次都击中目标的概率是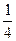 。
。
(Ⅰ)求乙、丙各自击中目标的概率。
(Ⅱ)求目标被击中的概率。