对于数列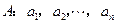 ,若满足
,若满足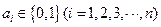 ,则称数列
,则称数列 为“0-1数列”.定义变换
为“0-1数列”.定义变换 ,
, 将“0-1数列”
将“0-1数列” 中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如
中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如 :1,0,1,则
:1,0,1,则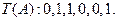 设
设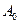 是“0-1数列”,令
是“0-1数列”,令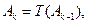
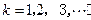 .
.
(Ⅰ) 若数列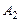 :
: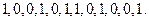 求数列
求数列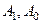 ;
;
(Ⅱ) 若数列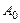 共有10项,则数列
共有10项,则数列 中连续两项相等的数对至少有多少对?请说明理由;
中连续两项相等的数对至少有多少对?请说明理由;
(Ⅲ)若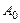 为0,1,记数列
为0,1,记数列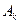 中连续两项都是0的数对个数为
中连续两项都是0的数对个数为 ,
, .求
.求 关于
关于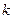 的表达式.
的表达式.
推荐套卷
对于数列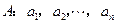 ,若满足
,若满足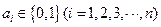 ,则称数列
,则称数列 为“0-1数列”.定义变换
为“0-1数列”.定义变换 ,
, 将“0-1数列”
将“0-1数列” 中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如
中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如 :1,0,1,则
:1,0,1,则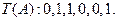 设
设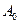 是“0-1数列”,令
是“0-1数列”,令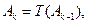
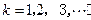 .
.
(Ⅰ) 若数列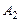 :
: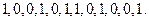 求数列
求数列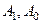 ;
;
(Ⅱ) 若数列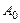 共有10项,则数列
共有10项,则数列 中连续两项相等的数对至少有多少对?请说明理由;
中连续两项相等的数对至少有多少对?请说明理由;
(Ⅲ)若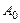 为0,1,记数列
为0,1,记数列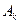 中连续两项都是0的数对个数为
中连续两项都是0的数对个数为 ,
, .求
.求 关于
关于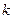 的表达式.
的表达式.