(本小题满分16 分)如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点.
分)如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点.
(1)求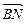 的长;
的长;
(2)求 的值;
的值;
(3)求证:A1B⊥C1M.
相关知识点
推荐套卷
(本小题满分16 分)如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点.
分)如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点.
(1)求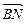 的长;
的长;
(2)求 的值;
的值;
(3)求证:A1B⊥C1M.