已知抛物线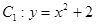
与圆
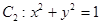
（I）求抛物线
上一点
与圆
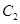上一动点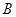
的距离的最小值；
（II）将圆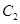向上平移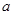
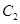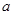个单位后能否使圆在抛物线内并触及抛物线（与相切于顶点）的底部？若能，请求出的值，若不能，试说明理由；
（III）设点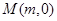
为
轴上一个动点，过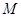
作抛物线的两条切线，切点分别为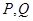
，求证：直线
过定点，并求出定点坐标。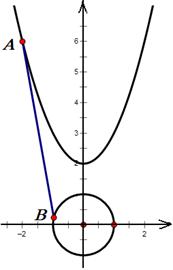
相关试题
的前
项和为
,
. 
,求数列
的前
项和
.
，
.
；
与
、
均相切，切点分别为（
）、（
），且
，求证：
.
.
的单调区间；
与
有三个不同的交点，求实数
的取值范围.
.
的最小正周期；
在
处取得最大值，求
的值;
的单调递增区间.
为等差数列，且
.
项和
；
满足
求数列相关知识点
推荐套卷
已知抛物线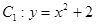与圆
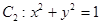
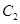（I）求抛物线上一点与圆上一动点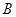的距离的最小值；
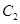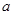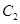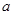（II）将圆向上平移个单位后能否使圆在抛物线内并触及抛物线（与相切于顶点）的底部？若能，请求出的值，若不能，试说明理由；
（III）设点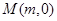为轴上一个动点，过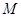作抛物线的两条切线，切点分别为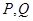，求证：直线过定点，并求出定点坐标。
粤公网安备 44130202000953号