（本小题满分14分）
函数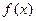
定义在区间[a, b]上，设“
”表示函数
在集合D上的最小值，“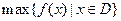
”表示函数在集合D上的最大值．现设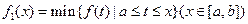
，
，
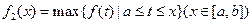若存在最小正整数k，使得
对任意的
成立，则称函数为区间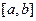
上的“第k类压缩函数”．
(Ⅰ) 若函数
，求的最大值，写出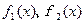
的解析式；
(Ⅱ) 若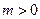
，函数
是
上的“第3类压缩函数”，求m的取值范围．
相关试题
外一点
引切线与⊙
，
为
的中点，过
两点. 求证：
,
在
上的单调递增；
有三个零点，求
的值；
恒成立，求a的取值范围。
.
的单调区间；
对
恒成立，求实数
的取值范围.
的各项均为正数，其前
项和为
，且
.
，求证：
；
，
，求
.
中，
，
，
，正方形
所在平面与平面
分别是
的中点。
平面
；
与平面推荐套卷
（本小题满分14分）
函数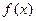定义在区间[a, b]上，设“”表示函数在集合D上的最小值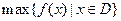，“”表示函数在集合D上的最大值．现设，，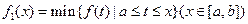
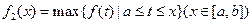若存在最小正整数k，使得对任意的成立，则称函数为区间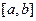上的“第k类压缩函数”．
(Ⅰ) 若函数，求的最大值，写出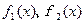的解析式；
(Ⅱ) 若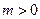，函数是上的“第3类压缩函数”，求m的取值范围．
粤公网安备 44130202000953号