已知直线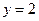
与函数
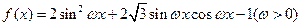的图像的两个相邻交点之间的距离为
。
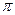（I）求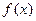
的解析式，并求出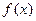的单调递增区间
（II）将函数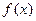的图像向左平移
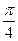个单位得到函数
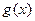的图像，求函数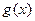的最大值及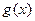取得最大值时x的取值集合。
相关试题
的前
项和为
已知
，证明数列
是等比数列；
的底面是正方形，
，点E在棱PB上.
； 
且
时，求AE与平面PDB所成的角的正切值.
的周长为
，且
．
的长；
，求角
的度数．
的顶点
、
、
，
边上的中线所在直线为
.
关于直线
，
在
上无极值，求
值；
上的最小值
表达式；
，任意的
，均有
成立，求
的取值范围.相关知识点
推荐套卷
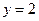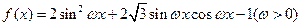已知直线与函数的图像的两个相邻交点之间的距离为。
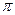（I）求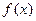的解析式，并求出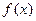的单调递增区间
（II）将函数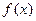的图像向左平移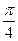个单位得到函数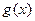的图像，求函数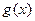的最大值及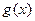取得最大值时x的取值集合。
粤公网安备 44130202000953号