在学习“轴对称现象”内容时，王老师让同学们寻找身边的轴对称图形，小明有一副三角尺和一个量角器（如图所示）．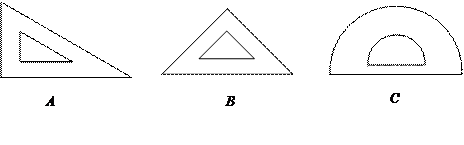
⑴小明的这三件文具中，可以看做是轴对称图形的是___________（填字母代号）；
⑵小红也有同样的一副三角尺和一个量角器．若他们分别从自己这三件文具中随机取出一件，则可以拼成一个轴对称图案的概率是多少？
相关试题
在平面直角坐标系中，O为坐标原点，点A坐标为（1，0），以OA为边在第一象限内作等边△OAB，C为x轴正半轴上的一个动点（OC＞1），连接BC，以BC为边在第一象限内作等边△BCD，直线DA交y轴于E点．
（1）如图，当C点在x轴上运动时，设AC＝x，请用x表示线段AD的长；
（2）随着C点的变化，直线AE的位置变化吗？若变化，请说明理由；若不变，请求出直线AE的解析式．
（3）以线段BC为直径作圆，圆心为点F，
①当C点运动到何处时直线EF∥直线BO？此时⊙F和直线BO的位置关系如何？请说明理由．
②G为CD与⊙F的交点，H为直线DF上的一个动点，连结HG、HC，求HG＋HC的最小值，并将此最小值用x表示．
已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D．
（1）如图①，当直线l与⊙O相切于点C时，若∠DAC=30°，求∠BAC的大小；
（2）如图②，当直线l与⊙O相交于点E、F时，若∠DAE=18°，求∠BAF的大小．
粤公网安备 44130202000953号