（本小题满分10分）选修4－l：几何证明选讲
如图所示，圆O的两弦AB和CD交于点E，EF∥CB，EF交AD的延长线于点F，FG切圆O于点G．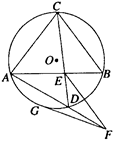
（Ⅰ）求证：△DFE∽△EFA；
（Ⅱ）如果FG＝1，求EF的长．
0，
.
值； (2)求
的值.
.
在闭区间
上的最大值是1？若存在，求出对应的a值？若不存在，试说明理由．
，x∈R(其中A＞0，ω＞0,
)的周期为π，且图象上一个最低点为M
.
时，求f(x)的最大值．
，
.
值； (2)求
的值.推荐套卷
（本小题满分10分）选修4－l：几何证明选讲
如图所示，圆O的两弦AB和CD交于点E，EF∥CB，EF交AD的延长线于点F，FG切圆O于点G．
（Ⅰ）求证：△DFE∽△EFA；
（Ⅱ）如果FG＝1，求EF的长．
粤公网安备 44130202000953号