（本小题满分12分）
已知函数f1（x）＝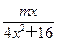
,f2（x）＝
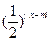（其中m ∈R且m≠0）.
（Ⅰ）讨论函数f1（x）的单调性；
（Ⅱ）若m<－2，求函数f（x）＝f1（x）＋f2（x）（x∈[－2，2]）的最值；
（Ⅲ）设函数g（x）＝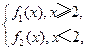
当m≥2时，若对于任意的x1∈[2，＋∞），总存在唯一的x2∈（－∞，2），使得g（x1）＝g（x2）成立．试求m的取值范围．
，n
，函数
m·n．
，求
的值；
，且满足
，求
相关知识点
推荐套卷
（本小题满分12分）
已知函数f1（x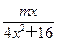）＝,f2（x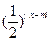）＝（其中m ∈R且m≠0）.
（Ⅰ）讨论函数f1（x）的单调性；
（Ⅱ）若m<－2，求函数f（x）＝f1（x）＋f2（x）（x∈[－2，2]）的最值；
（Ⅲ）设函数g（x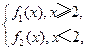）＝当m≥2时，若对于任意的x1∈[2，＋∞），总存在唯一的x2∈（－∞，2），使得g（x1）＝g（x2）成立．试求m的取值范围．
粤公网安备 44130202000953号