(本小题满分12分)
已知椭圆C1和抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点,从它们每条曲线 上至少取两个点,将其坐标记录于下表中:
上至少取两个点,将其坐标记录于下表中:
| x |
5 |
-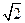 |
4 |
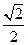 |
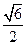 |
| y |
2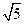 |
0 |
-4 |
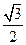 |
-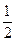 |

(Ⅰ)求C1和C2的方程;
(Ⅱ)过点S(0,-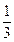 )且斜率为k的动直线l交椭圆C1于A、B两点,在y轴上是否存在定点D,使以线段AB为直径的圆恒过这个点?若存在,求出D的坐标,若不存在,说明理由.
)且斜率为k的动直线l交椭圆C1于A、B两点,在y轴上是否存在定点D,使以线段AB为直径的圆恒过这个点?若存在,求出D的坐标,若不存在,说明理由.
相关知识点
推荐套卷
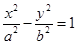 (a>b>0)的一个焦点为
(a>b>0)的一个焦点为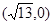 ,离心率为
,离心率为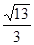 .
. =(sin(
=(sin(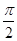 +x),
+x),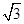 cosx),
cosx), =(sinx,cosx), f(x)=
=(sinx,cosx), f(x)= 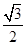 ,求角A的值.
,求角A的值. 中,角
中,角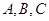 的对边分别为
的对边分别为 ,
,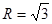 ,且满足
,且满足
 和边
和边 的大小;
的大小;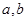 为正整数(
为正整数(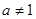 ),等差数列
),等差数列 的首项为
的首项为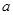 ,公差为
,公差为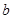 , 等比数列
, 等比数列 的首项为
的首项为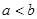 ,且
,且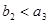 .在数列
.在数列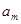 与
与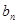 有
有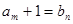 ,又设
,又设 .
. 为等差数列,求常数
为等差数列,求常数 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号