（本小题满分12分）
已知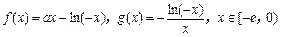
．
（1）讨论a =" –" 1时，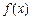
的单调性、极值；
（2）求证：在(1)的条件下，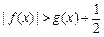
；
（3）是否存在实数a，使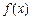的最小值是3，如果存在，求出a的值；若不存在，
请说明理
由．
，求函数的最小值与最大值
B.
，
，求
及
相关知识点
推荐套卷
（本小题满分12分）
已知．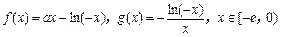
（1）讨论a =" –" 1时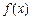，的单调性、极值；
（2）求证：在(1)的条件下，；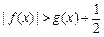
（3）是否存在实数a，使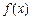的最小值是3，如果存在，求出a的值；若不存在，
请说明理由．
粤公网安备 44130202000953号