(本小题满分12分)
如图,多面体ABCD—EFG中,底面 ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:
ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:
(I)求证:平面AEF⊥平面BDG;
(II)若存在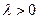 使得
使得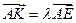 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为 ,求
,求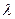 的值。
的值。
推荐套卷
(本小题满分12分)
如图,多面体ABCD—EFG中,底面 ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:
ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:
(I)求证:平面AEF⊥平面BDG;
(II)若存在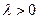 使得
使得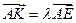 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为 ,求
,求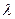 的值。
的值。