．（本小题满分12分）
为了调查某中学高三学生的身高情况，在该中学高三学生中随机抽取了40名同学作为样本，测得他们的身高后，画出频率分布直方图如下：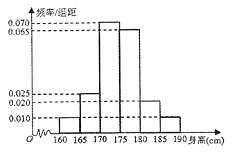
（I）估计该校高三学生的平均身高；
（II）从身高在180cm（含180cm）以上的样本中随机抽取2人，记身高在185~190cm之间的人数为X，求X的分布列和数学期望。
相关试题
}中，
，且
，
的值；
展开式中的所有二项式系数和为512，
（
且
）.
时，求证:
在
上单调递增；
且
时,求证:
.
，曲线
.自曲线
上一点
作
的两条切线切点分别为
.
，求
；
的最大值.
平面
,
为等边三角形.
，求证：平面
平面
；
的体积为
,求此时二面角
的余弦值.相关知识点
推荐套卷
．（本小题满分12分）
为了调查某中学高三学生的身高情况，在该中学高三学生中随机抽取了40名同学作为样本，测得他们的身高后，画出频率分布直方图如下：
（I）估计该校高三学生的平均身高；
（II）从身高在180cm（含180cm）以上的样本中随机抽取2人，记身高在185~190cm之间的人数为X，求X的分布列和数学期望。
粤公网安备 44130202000953号