((本小题满分12分)
由倍角公式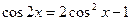 ,可知
,可知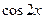 可以表示为
可以表示为 的二次多项式.
的二次多项式.
对于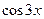 ,我们有
,我们有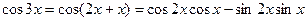
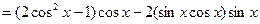
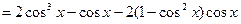

可见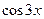 可以表示为
可以表示为 的三次多项式。一般地,存在一个
的三次多项式。一般地,存在一个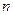 次多项式
次多项式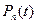 ,使得
,使得 ,这些多项式
,这些多项式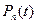 称为切比雪夫多项式.
称为切比雪夫多项式.
(I)求证: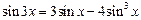 ;
;
(II)请求出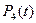 ,即用一个
,即用一个 的四次多项式来表示
的四次多项式来表示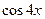 ;
;
(III)利用结论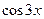
 ,求出
,求出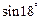 的值.
的值.
推荐套卷
((本小题满分12分)
由倍角公式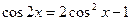 ,可知
,可知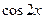 可以表示为
可以表示为 的二次多项式.
的二次多项式.
对于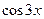 ,我们有
,我们有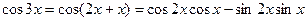
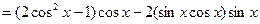
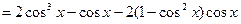

可见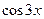 可以表示为
可以表示为 的三次多项式。一般地,存在一个
的三次多项式。一般地,存在一个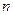 次多项式
次多项式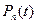 ,使得
,使得 ,这些多项式
,这些多项式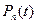 称为切比雪夫多项式.
称为切比雪夫多项式.
(I)求证: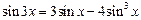 ;
;
(II)请求出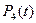 ,即用一个
,即用一个 的四次多项式来表示
的四次多项式来表示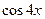 ;
;
(III)利用结论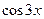
 ,求出
,求出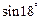 的值.
的值.