(提示:1、12、13、14班同学请完成试题(B),其他班级同学任选试题(A)或(B)作答)
(A) 已知点A(2,3),B(5,4),C(7,10)及 ,试问:
,试问:
(1)t为何值时,P在第三象限?
(2)是否存在D点使得四边形ABCD为平行四边形,若存在,求出D点坐标.
(B) 已知平行四边形ABCD,对角线AC与BD交于点E,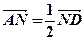 ,连接BN交AC于M,
,连接BN交AC于M,
(1)若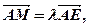 求实数λ.
求实数λ.
(2)若B(0,0),C(1,0),D(2,1),求M的坐标
推荐套卷
(提示:1、12、13、14班同学请完成试题(B),其他班级同学任选试题(A)或(B)作答)
(A) 已知点A(2,3),B(5,4),C(7,10)及 ,试问:
,试问:
(1)t为何值时,P在第三象限?
(2)是否存在D点使得四边形ABCD为平行四边形,若存在,求出D点坐标.
(B) 已知平行四边形ABCD,对角线AC与BD交于点E,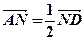 ,连接BN交AC于M,
,连接BN交AC于M,
(1)若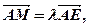 求实数λ.
求实数λ.
(2)若B(0,0),C(1,0),D(2,1),求M的坐标