（本小题满分16分）
如图，实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成，圆P和圆Q的半径都是2km，点P在圆Q上，现
要在公园内建一块顶点都在圆P上的多边形活动场地．
（1）如图甲，要建的活动场地为△RST，求场地的最大面积；
（2）如图乙，要建的活动场地为等腰梯形ABCD，求场地的最大面积．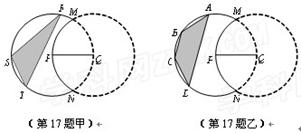
，
，函数
，若
且
，求
的值；
)的值；
∈(0，
)，f (
)＝
，求cos2
<
<
<
,
的值.（Ⅱ）求推荐套卷
（本小题满分16分）
如图，实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成，圆P和圆Q的半径都是2km，点P在圆Q上，现要在公园内建一块顶点都在圆P上的多边形活动场地．
（1）如图甲，要建的活动场地为△RST，求场地的最大面积；
（2）如图乙，要建的活动场地为等腰梯形ABCD，求场地的最大面积．
粤公网安备 44130202000953号