如图,面积为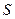 的正方形
的正方形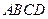 中有一个不规则的图形
中有一个不规则的图形 ,可按下面方法估计
,可按下面方法估计 的面积:在正方形
的面积:在正方形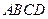 中随机投掷
中随机投掷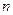 个点,若
个点,若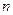 个点中有
个点中有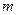 个点落入
个点落入 中,则
中,则 的面积的估计值为
的面积的估计值为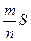 ,假设正方形
,假设正方形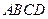 的边长为2,
的边长为2, 的面积为1,并向正方形
的面积为1,并向正方形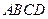 中随机投掷
中随机投掷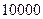 个点,以
个点,以 表示落入
表示落入 中的点的数目.
中的点的数目.
(I)求 的均值
的均值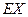 ;
;
(II)求用以上方法估计 的面积时,
的面积时, 的面积的估计值与实际值之差在区间
的面积的估计值与实际值之差在区间 内的概率.
内的概率.
附表: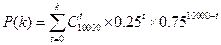
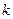 |
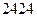 |
 |
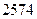 |
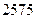 |
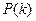 |
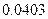 |
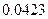 |
 |
 |
推荐套卷
如图,面积为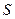 的正方形
的正方形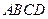 中有一个不规则的图形
中有一个不规则的图形 ,可按下面方法估计
,可按下面方法估计 的面积:在正方形
的面积:在正方形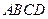 中随机投掷
中随机投掷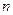 个点,若
个点,若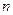 个点中有
个点中有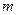 个点落入
个点落入 中,则
中,则 的面积的估计值为
的面积的估计值为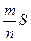 ,假设正方形
,假设正方形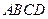 的边长为2,
的边长为2, 的面积为1,并向正方形
的面积为1,并向正方形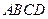 中随机投掷
中随机投掷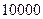 个点,以
个点,以 表示落入
表示落入 中的点的数目.
中的点的数目.
(I)求 的均值
的均值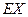 ;
;
(II)求用以上方法估计 的面积时,
的面积时, 的面积的估计值与实际值之差在区间
的面积的估计值与实际值之差在区间 内的概率.
内的概率.
附表: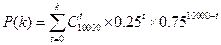
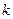 |
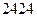 |
 |
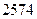 |
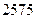 |
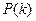 |
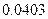 |
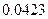 |
 |
 |