(本小题满分14分)
有 个首项都是1的等差数列,设第
个首项都是1的等差数列,设第 个数列的第
个数列的第 项为
项为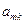
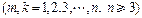 ,公差为
,公差为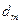
 ,并且
,并且 成等差数列.
成等差数列.
(Ⅰ)证明 (
(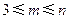 ,
,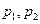 是
是
 的多项式),并求
的多项式),并求 的值
的值
(Ⅱ)当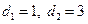 时,将数列
时,将数列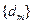 分组如下:
分组如下: (每组数的个数构成
(每组数的个数构成 等差数列).
等差数列).
设前 组中所有数之和为
组中所有数之和为 ,求数列
,求数列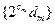 的前
的前 项和
项和 .
.
(Ⅲ)设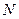 是不超过20的正整数,当
是不超过20的正整数,当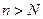 时,对于(Ⅱ)中的
时,对于(Ⅱ)中的 ,求使得不等式
,求使得不等式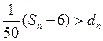 成立的所有
成立的所有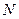 的值.
的值.
推荐套卷
(本小题满分14分)
有 个首项都是1的等差数列,设第
个首项都是1的等差数列,设第 个数列的第
个数列的第 项为
项为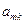
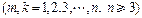 ,公差为
,公差为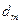
 ,并且
,并且 成等差数列.
成等差数列.
(Ⅰ)证明 (
(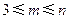 ,
,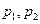 是
是
 的多项式),并求
的多项式),并求 的值
的值
(Ⅱ)当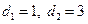 时,将数列
时,将数列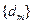 分组如下:
分组如下: (每组数的个数构成
(每组数的个数构成 等差数列).
等差数列).
设前 组中所有数之和为
组中所有数之和为 ,求数列
,求数列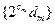 的前
的前 项和
项和 .
.
(Ⅲ)设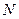 是不超过20的正整数,当
是不超过20的正整数,当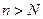 时,对于(Ⅱ)中的
时,对于(Ⅱ)中的 ,求使得不等式
,求使得不等式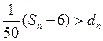 成立的所有
成立的所有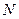 的值.
的值.