((本小题满分12分)
在平面直角坐标系xoy中,椭圆E: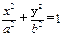 (a>0,b>0)经过点A(
(a>0,b>0)经过点A(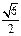 ,
,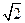 ),且点F(0,-1)为其一个焦点.
),且点F(0,-1)为其一个焦点.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设椭圆E与y轴的两 个交点为A1,A2,不在y轴上的动点P在直线y=b2上运动,直线PA1,PA2分别与椭圆E交于点M,N,证明:直线MN通过一个定点,且△FMN的周长为定值.
个交点为A1,A2,不在y轴上的动点P在直线y=b2上运动,直线PA1,PA2分别与椭圆E交于点M,N,证明:直线MN通过一个定点,且△FMN的周长为定值.
推荐套卷
((本小题满分12分)
在平面直角坐标系xoy中,椭圆E: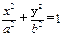 (a>0,b>0)经过点A(
(a>0,b>0)经过点A(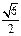 ,
,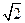 ),且点F(0,-1)为其一个焦点.
),且点F(0,-1)为其一个焦点.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设椭圆E与y轴的两 个交点为A1,A2,不在y轴上的动点P在直线y=b2上运动,直线PA1,PA2分别与椭圆E交于点M,N,证明:直线MN通过一个定点,且△FMN的周长为定值.
个交点为A1,A2,不在y轴上的动点P在直线y=b2上运动,直线PA1,PA2分别与椭圆E交于点M,N,证明:直线MN通过一个定点,且△FMN的周长为定值.