(本题6分)某学校组织课外活动小组,其中三个小组的人员分布如下表(每名同学只参加一个小组):
| |
棋类小组 |
书法小组 |
摄影小组 |
| 高中 |
a |
6 |
12 |
| 初中 |
7 |
4 |
18 |
学校要对这三个小组的活动 效果进行抽样调查,按分层抽样的方法从小组成员中抽取6人,结果摄影小组被抽出3人。
效果进行抽样调查,按分层抽样的方法从小组成员中抽取6人,结果摄影小组被抽出3人。
(Ⅰ)求a的值;
(Ⅱ)从书法小组的人中,随机选出3人参加书法比赛,求这3人中初、高中学生都有的概率。
推荐套卷
 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率; 表示获奖的人数,求
表示获奖的人数,求 ,
, 的值.
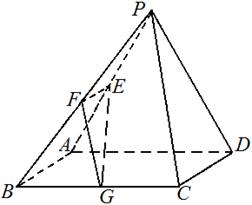
的值. 平面PAD;
平面PAD; ?
?
 的最大值为
的最大值为 ,
,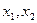 是集合
是集合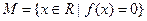 中的任意两个元素,且|
中的任意两个元素,且|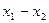 |的最小值为
|的最小值为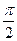 。
。 ,
, 的值;
的值;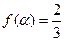 ,求
,求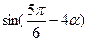 的值
的值 R,函数
R,函数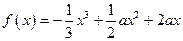 (x∈R).
(x∈R).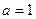 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;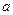 的取值范围;若不是,请说明理由;
的取值范围;若不是,请说明理由; 上单调递增,求
上单调递增,求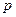 与日产量
与日产量 (
( )件间的关系为
)件间的关系为  ,每生产一件正品盈利2900元,每出现一件次品亏损1100元.
,每生产一件正品盈利2900元,每出现一件次品亏损1100元.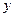 (元)表示为日产量
(元)表示为日产量 量为多少件时,日利润最大?
量为多少件时,日利润最大? )
) 粤公网安备 44130202000953号
粤公网安备 44130202000953号