(本小题满分13分)
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽样100名志原者的年龄情况如下表所示。
(Ⅰ)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图(如图),再根据频率分布直方图估计这500名志愿者中年龄在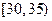 岁的人数;
岁的人数;
(Ⅱ)在抽出的100名志原者中按年龄再采用分层抽样法抽取20人参加中心广场的宣传活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望。
推荐套卷
 平面ABC ,
平面ABC , ,已知AE与平面ABC所成的角为
,已知AE与平面ABC所成的角为 ,
, 且
且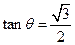 .
.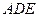 ;
;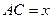 ,
, 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求 枪,每一枪的射击结果相互独立,每枪成绩不低于10环的概率为
枪,每一枪的射击结果相互独立,每枪成绩不低于10环的概率为 ,设
,设 为本次训练中成绩不低于10环的射击次数,
为本次训练中成绩不低于10环的射击次数,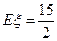 ,方差
,方差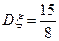 .
.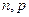 的值;
的值; ,
,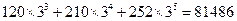 )
)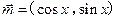 ,
,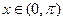 ,
, .
. ,求
,求 的值;
的值; ,求函数
,求函数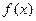 的值域.
的值域.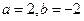 ,求函数
,求函数 的极值;
的极值; 是函数
是函数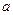 关于
关于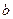 的关系式(用
的关系式(用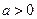 ,函数
,函数 .若存在
.若存在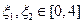 使得
使得 成立,求
成立,求 和
和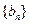 满足
满足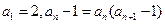 ,
, ,
, .
.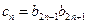 ,求使得
,求使得
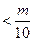 对一切
对一切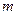 ;
; 和为
和为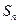 ,
,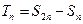 ,试比较
,试比较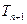 与
与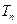 的大小.
的大小. 粤公网安备 44130202000953号
粤公网安备 44130202000953号