本小题共13分)
对数列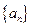
，规定
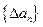为数列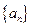的一阶差分数列，其中
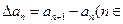N*)．对正整数k，规定
为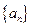的k阶差分数列，其中
．
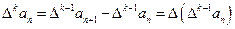（Ⅰ）若数列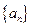的首项
，且满足
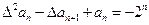，求数列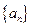的通项公式；
（Ⅱ）对（Ⅰ）中的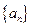数列，若数列
是等差数列，使得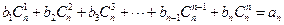
对一切正整数
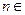N*都成立，求
；
（Ⅲ）在（Ⅱ）的条件下，令
设
若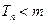
成立，求最小正整数
的值．
相关试题
;
+
≥8;
+ 
≥
;
≥
.
，求x(4-3x)的最大值；
的最大值.
+
+
≥9.
+
=1,求x+y的最小值；
,求函数y=4x-2+
的最大值；相关知识点
推荐套卷
本小题共13分)
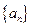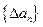对数列，规定为数列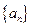的一阶差分数列，其中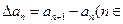N*)．对正整数k，规定为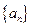的k阶差分数列，其中．
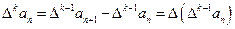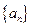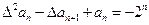（Ⅰ）若数列的首项，且满足，求数列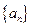的通项公式；
（Ⅱ）对（Ⅰ）中的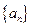数列，若数列是等差数列，使得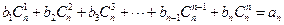对一切正整数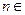N*都成立，求；
（Ⅲ）在（Ⅱ）的条件下，令设若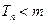成立，求最小正整数的值．
粤公网安备 44130202000953号