已知函数f(x)=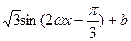
,且该函数图像的对称中心到对称轴的最小距离为
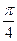当
时,f(x)的最大值为1。
(1) 
求函数f(x)的解析式.
(2) 若f(x)-3≤m≤f(x)+3在
上恒成立,求m的范围.
相关试题
（1）求不等式
的解集；
的解集是非空集合，求实数m的取值范围.
直线
的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程；如图，BA是圆O的直径，延长BA至E，使得AE=AO,过E点作圆O的割线交圆O于D、E，使AD=DC,
求证：
;
若ED=2，求圆O的内接四边形ABCD的周长。
，
在
上的最小值；
与
的图像恰有一个公共点，求实数a的值；
有两个不同的极值点
，且
，求实数a的取值范围。
是椭圆的左、右焦点，O为坐标原点，点P
在椭圆上，线段
与y轴的交点M满足
为直径的圆，直线
：
与圆相切，并与椭圆交于不同的两点
,当
,且满足
时，求直线相关知识点
推荐套卷
已知函数f(x)=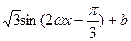,且该函数图像的对称中心到对称轴的最小距离为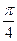当时,f(x)的最大值为1。
(1) 求函数f(x)的解析式.
(2) 若f(x)-3≤m≤f(x)+3在上恒成立,求m的范围.
如图，BA是圆O的直径，延长BA至E，使得AE=AO,过E点作圆O的割线交圆O于D、E，使AD=DC,
求证：;
若ED=2，求圆O的内接四边形ABCD的周长。
粤公网安备 44130202000953号