（本小题满分12分）
如图，在三棱锥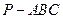
中，
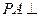底面ABC,
，
AP="AC," 点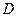
，
分别在棱
上，且BC//平面ADE
（Ⅰ）求
证：DE⊥平面
；
（Ⅱ）当二面角
为直二面角时，求多面体ABCED与PAED的体积比。
相关试题
asinC－ccosA.
满足
，且
成等比数列。
；
为数列
的前n项和
。
的定义域及最小正周期；
.
的单调性；
.如果对任意
，
，求
的取值范围.
中，
是抛物线
的焦点，
是抛物线
上位于第一象限内的任意一点，过
三点的圆的圆心为
，点
．（Ⅰ）求抛物线
与抛物线
若存在，求出点推荐套卷
（本小题满分12分）
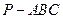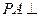如图，在三棱锥中，底面ABC,，
AP="AC," 点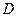，分别在棱上，且BC//平面ADE
（Ⅰ）求证：DE⊥平面；
（Ⅱ）当二面角为直二面角时，求多面体ABCED与PAED的体积比。
粤公网安备 44130202000953号