（1）已知公差不为0的数列{an}的首项a1=1，前n项的和为Sn，若数列{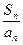
}是等差数列，
①求an；②令bn=qSn（q>0）,若对一切n∈N*，都有
>2bn*bn+2，求q的取值范围。
（2）是否存在各项都是正整数的无穷数列{cn}，使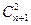
>2Cn*Cn+2对一切n∈N*都成立，若存在，请写出数列的一个通项公式，若不存在，说明理由。
相关试题
为偶函数，曲线
过点
，
．
存在斜率为0的切线，求实数
的取值范围；
时函数
过点
，且与曲线
和
都相切，
的值。
是定义在R上的偶函数，其图象关于
对称，对任意的
，都有
，且
；
．
的图象过原点，且在原点处的切线斜率是
，求
的值；
上不单调，求
的取值范围．
求
的单调区间； 
若
处取得极值，直线
与
的图象有三个不同的交点，求
的取值范围。推荐套卷
（1）已知公差不为0的数列{an}的首项a1=1，前n项的和为Sn，若数列{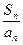}是等差数列，
①求an；②令bn=qSn（q>0）,若对一切n∈N*，都有>2bn*bn+2，求q的取值范围。
（2）是否存在各项都是正整数的无穷数列{cn}，使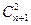>2Cn*Cn+2对一切n∈N*都成立，若存在，请写出数列的一个通项公式，若不存在，说明理由。
粤公网安备 44130202000953号