 如图扇形AOB是一个观光区的平面示意图,其中∠AOB的圆心角为
如图扇形AOB是一个观光区的平面示意图,其中∠AOB的圆心角为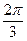 ,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成。其中D在线段OB上,且CD//AO,设∠AOC=θ,
,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成。其中D在线段OB上,且CD//AO,设∠AOC=θ,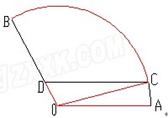
(1)用θ表示CD的长度,并写出θ的取值范围。
(2)当θ为何值时,观光道路最长?
相关知识点
推荐套卷
 如图扇形AOB是一个观光区的平面示意图,其中∠AOB的圆心角为
如图扇形AOB是一个观光区的平面示意图,其中∠AOB的圆心角为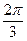 ,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成。其中D在线段OB上,且CD//AO,设∠AOC=θ,
,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成。其中D在线段OB上,且CD//AO,设∠AOC=θ,
(1)用θ表示CD的长度,并写出θ的取值范围。
(2)当θ为何值时,观光道路最长?