如图, 椭圆C：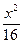
+
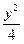=1的右顶点是A，上下两个顶点分别为B、D，四边形DAMB是矩形（O为坐标原点）
，点E、P分别是线段OA、AM的中点。
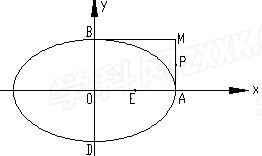
（1）求证：直线DE与直线BP的交点在椭圆C上.
（2）过点B的直线l1、l2与椭圆C分别交于R、S（不同于B点），且它们的斜率k1、k2满足k1*k2=-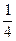
，求证：直线RS过定点，并求出此定点的坐标。
相关试题
、
、
分别为空间四边形
的边
，
，
上的点，且
．
平面
，
平面
的交线
．
中，求证：平面
平面
．
中，试作出过
且与直线
平行的截面，并说明理由．
的边长为
，平面
到正方形各顶点的距离都是
，
分别是
，
上的点，且
．
平面
；
的长．
为
所在平面外一点，
，
分别是
，
的中点，平面
平面
．
．
与平面
是否平行？试证明你的结论．
推荐套卷
如图, 椭圆C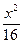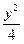：+=1的右顶点是A，上下两个顶点分别为B、D，四边形DAMB是矩形（O为坐标原点），点E、P分别是线段OA、AM的中点。
（1）求证：直线DE与直线BP的交点在椭圆C上.
（2）过点B的直线l1、l2与椭圆C分别交于R、S（不同于B点），且它们的斜率k1、k2满足k1*k2=-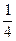，求证：直线RS过定点，并求出此定点的坐标。
粤公网安备 44130202000953号