（（本小题满分12分）
已知圆C：x2+(y－1)2 =5，直线l：mx－y+l－m=0，
（1）求证：对任意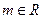
，直线l与圆C总有两个不同的交点。
（2）设l与圆C交于A、B两点，若| AB | =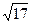 
，求l的倾斜角；
（3）求弦AB的中点M的轨迹方程；
，且
是奇函数．
，
的值；（Ⅱ）求函数
的单调区间．
.
的焦点是F，点P是抛物线上的动点，又有点A（3,2），求
最小值，并求此时P点的坐标.相关知识点
推荐套卷
（（本小题满分12分）
已知圆C：x2+(y－1)2 =5，直线l：mx－y+l－m=0，
（1）求证：对任意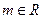，直线l与圆C总有两个不同的交点。
（2）设l与圆C交于A、B两点，若| AB | = 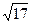，求l的倾斜角；
（3）求弦AB的中点M的轨迹方程；
粤公网安备 44130202000953号