如图，四棱锥P－ABCD中，PA⊥底
面ABCD，
∥
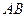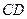，AD＝CD＝1，∠
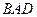=120°，
=
，∠
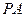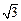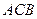=90°，M是线段PD上的一点（不包括端点)．
（1）求证：BC⊥平面PAC；
（2）求异面直线AC与PD所成的角的余弦值；
（3）若点M为侧棱PD中点，求直线MA与平面PCD
所成角的正弦值．
相关试题
， B
， C
，且
，
表示
,试在下坐标系中画出
图像的示意图，并据此回答：不等式
的解集.
为三角形的一个内角，符合条件：
，求
且
求
的最大值.
，
时，
.
(a＞c＞b)的两根之差的平方等于4，△ABC的面积S＝10
，c＝7.
的值.推荐套卷
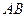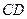如图，四棱锥P－ABCD中，PA⊥底面ABCD，∥，AD＝CD＝1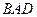，∠=120°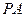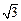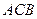，=，∠=90°，M是线段PD上的一点（不包括端点)．
（1）求证：BC⊥平面PAC；
（2）求异面直线AC与PD所成的角的余弦值；
（3）若点M为侧棱PD中点，求直线MA与平面PCD
所成角的正弦值．
粤公网安备 44130202000953号