(本小题15分)
先阅读下列不等式的证法,再解决后面的问题:已知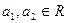 且
且 ,求证
,求证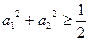
证明:构造 函数
函数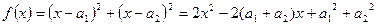 因为对一切
因为对一切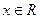 ,恒有
,恒有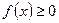 ,所以
,所以 4-8
4-8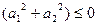 ,从而
,从而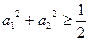
(1)若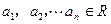 ,且
,且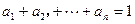 ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述证法,对你的结论加以证明;
(3)若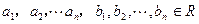 ,求证
,求证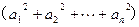
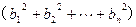
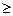
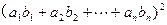 .[
.[
相关知识点
推荐套卷
(本小题15分)
先阅读下列不等式的证法,再解决后面的问题:已知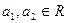 且
且 ,求证
,求证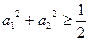
证明:构造 函数
函数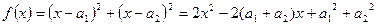 因为对一切
因为对一切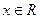 ,恒有
,恒有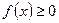 ,所以
,所以 4-8
4-8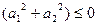 ,从而
,从而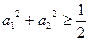
(1)若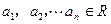 ,且
,且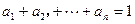 ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述证法,对你的结论加以证明;
(3)若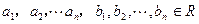 ,求证
,求证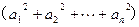
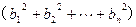
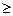
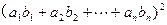 .[
.[