（本小题满分14分）
抛物线D以双曲线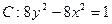
的焦点
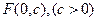为焦点
．
（1）求抛物线D的
标准方程；
（2）过直线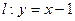
上的动点P作抛物线D的两条切线，切点为A，B．求证：直线AB过定点Q，并求出Q的坐
标；
（3）在（2）的条件下，若直线PQ交抛物线D于M，N两点，求证：|PM|·|QN|=|QM|·|PN|
|
,
∈N+}，集合B={
|
,
∈N+}，试证：A
B．
，若
，求p的取值范围。
A，求实数p的取值范围．
，
，若
，求实数a组成的集合的子集有多少个？相关知识点
推荐套卷
（本小题满分14分）
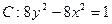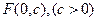抛物线D以双曲线的焦点为焦点．
（1）求抛物线D的标准方程；
（2）过直线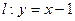上的动点P作抛物线D的两条切线，切点为A，B．求证：直线AB过定点Q，并求出Q的坐标；
（3）在（2）的条件下，若直线PQ交抛物线D于M，N两点，求证：|PM|·|QN|=|QM|·|PN|
粤公网安备 44130202000953号