(本小题14分)已知点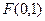 ,直线
,直线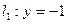 ,
,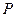 为平面上的动点,过点
为平面上的动点,过点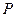 作直线
作直线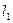 的垂线,垂足为点
的垂线,垂足为点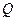 ,且
,且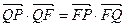 .
.
(1)求动点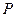 的轨迹
的轨迹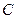 的方程;
的方程;
(2)轨迹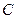 上是否存在一点
上是否存在一点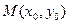 使得过
使得过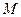 的切线
的切线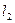 与直线
与直线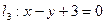 平行?若存在,求出
平行?若存在,求出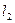 的方程,并求出它与
的方程,并求出它与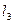 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.
推荐套卷
(本小题14分)已知点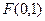 ,直线
,直线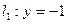 ,
,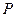 为平面上的动点,过点
为平面上的动点,过点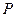 作直线
作直线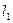 的垂线,垂足为点
的垂线,垂足为点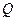 ,且
,且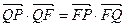 .
.
(1)求动点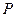 的轨迹
的轨迹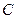 的方程;
的方程;
(2)轨迹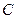 上是否存在一点
上是否存在一点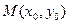 使得过
使得过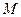 的切线
的切线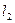 与直线
与直线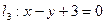 平行?若存在,求出
平行?若存在,求出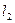 的方程,并求出它与
的方程,并求出它与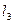 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.