如图,是一个用六根竹条连接而成的凸六边形风筝骨架,考虑到骨架的稳固性、美观性、实用性等因素,需再加竹条与其顶点连接。要求:
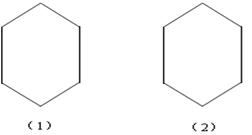
(1)在图(1)、(2)中分别加适当根竹条,设计出两种不同的连接方案。
(2)通过上面的设计,可以看出至少需再加 根竹条,才能保证风筝骨架稳固、美观和实用。(3)在上面的方案设计过程中,你所应用的数学道理是
相关知识点
推荐套卷
如图,是一个用六根竹条连接而成的凸六边形风筝骨架,考虑到骨架的稳固性、美观性、实用性等因素,需再加竹条与其顶点连接。要求:

(1)在图(1)、(2)中分别加适当根竹条,设计出两种不同的连接方案。
(2)通过上面的设计,可以看出至少需再加 根竹条,才能保证风筝骨架稳固、美观和实用。(3)在上面的方案设计过程中,你所应用的数学道理是