（本小题满分14分）
如图，在四棱锥P-ABCD中，PD上⊥平面ABCD，AD⊥CD，且BD平分∠ADC，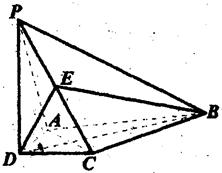
E为PC的中点，AD=CD=l，BC=PC，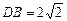
(Ⅰ)证明PA∥平面BDE；
(Ⅱ)证明AC⊥平面PBD：
(Ⅲ)求四棱锥P-ABCD的体积，
－
≥a＋
－2.
≥
＋
.
(n>1，n∈N*)的过程中，用n＝k＋1时左边的代数式减去n＝k时左边的代数式的结果是A，求代数式A.推荐套卷
（本小题满分14分）
如图，在四棱锥P-ABCD中，PD上⊥平面ABCD，AD⊥CD，且BD平分∠ADC， E为PC的中点，AD=CD=l，BC=PC，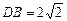
(Ⅰ)证明PA∥平面BDE；
(Ⅱ)证明AC⊥平面PBD：
(Ⅲ)求四棱锥P-ABCD的体积，
粤公网安备 44130202000953号