（本小题满分12分）
如图，四棱锥S—ABCD的底面是边长为1的正方形，SD垂直于底面ABCD，SB=
．
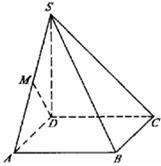
（Ⅰ）求面ASD与面BSC所成二面角的大小；
（Ⅱ）设棱SA的中点为M，求异面直线DM与SB所成角的大小；
（Ⅲ）求点D到平面SBC的距离．
相关试题
（本小题满分12分）在
中，边a，b，c的对角分别为A，B，C；且
，面积
．
（Ⅰ）求a的值；
（Ⅱ）设
，将
图象上所有点的横坐标变为原来的
（纵坐标不变）得到
的图象，求的单调增区间．
（其中
）．
的极值；
上的最小值；
，判断函数
零点个数．
的前
项和为
，
．
的前
,
，点
在直线
上，若存在
，使不等式
成立，求实数
的最大值．
且
时，判断
与
的大小，并给出证明．
在
处切线与直线
垂直．
解析式；
的大致图象．推荐套卷
粤公网安备 44130202000953号