（本小题满分13分）
已知函数
（1）如果对任意
恒成立，求实数a的取值范围；
（2）设实数
的两个极
值点分别为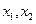
判断①
②
③
是否为定值？若是定值请求出；若不是定值，请把不是定
值的表示为函数
并求出
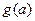的最小值；
（3）对于（2）中的设
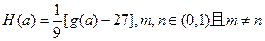，试比较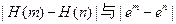
（e为自然对数的底）的大小，并证明。
方程；
的单调区间.
，求
;
，求实数
.
的前
项和为
，且
，
及前
的前14项和
。
，
的最大值和最小正周期；
为
的三个内角，若
，且
为锐角，求
的值。
中，角
所对的边是
，且满足
。
的大小；
，求
的最小值。推荐套卷
（本小题满分13分）
已知函数
（1）如果对任意恒成立，求实数a的取值范围；
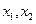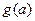（2）设实数的两个极值点分别为判断①②③是否为定值？若是定值请求出；若不是定值，请把不是定值的表示为函数并求出的最小值；
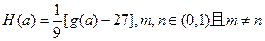（3）对于（2）中的设，试比较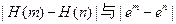（e为自然对数的底）的大小，并证明。
粤公网安备 44130202000953号