(本小题满分12分)
已知平行六面体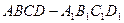 的底面为正方形,
的底面为正方形,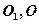 分别为上、下底面的中心,且
分别为上、下底面的中心,且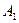 在底面
在底面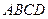 的射影是
的射影是 。
。 (Ⅰ)求证:平面
(Ⅰ)求证:平面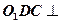 平面
平面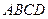 ;
;
(Ⅱ)若点 分别在棱上
分别在棱上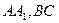 上,且
上,且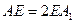 ,问点
,问点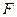 在何处时,
在何处时,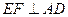 ;
;
(Ⅲ)若 ,求二面角
,求二面角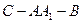 的大小(用反三角函数表示)。
的大小(用反三角函数表示)。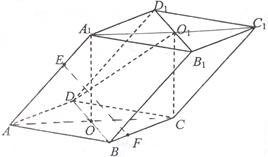
推荐套卷
(本小题满分12分)
已知平行六面体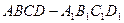 的底面为正方形,
的底面为正方形,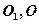 分别为上、下底面的中心,且
分别为上、下底面的中心,且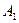 在底面
在底面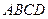 的射影是
的射影是 。
。 (Ⅰ)求证:平面
(Ⅰ)求证:平面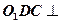 平面
平面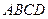 ;
;
(Ⅱ)若点 分别在棱上
分别在棱上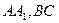 上,且
上,且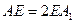 ,问点
,问点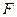 在何处时,
在何处时,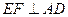 ;
;
(Ⅲ)若 ,求二面角
,求二面角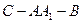 的大小(用反三角函数表示)。
的大小(用反三角函数表示)。