(本小题满分12分)
盒中有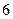
个小球,
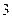个白球,记为
，
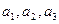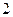个红球, 记为
，
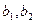个黑球, 记为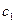
，除了颜色和编号外,球没有任何区别.
(1) 求从盒中取一球是红球的概率；
(2) 从盒中取一球，记下颜色后放回，再取一球，记下颜色，若取白球得分，取红球得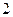分，取黑球得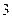分，求两次取球得分之和为
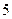分的概率
相关试题
，n
，函数
m·n．
，求
的值；
，且满足
，求
最小值；推荐套卷
(本小题满分12分)
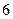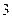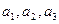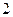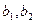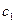盒中有个小球,个白球,记为，个红球, 记为，个黑球, 记为，除了颜色和编号外,球没有任何区别.
(1) 求从盒中取一球是红球的概率；
(2) 从盒中取一球，记下颜色后放回，再取一球，记下颜色，若取白球得分，取红球得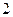分，取黑球得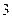分，求两次取球得分之和为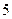分的概率
粤公网安备 44130202000953号