已知圆o：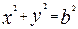
与椭圆
有一个公共点A（0，1），F为椭圆的左焦点，直线AF被圆所截得的弦长为1.
（1）求椭圆方程。
（2）圆o与ｘ轴的两个交点为C、D，B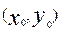
是椭圆上异于点A的一个动点，在线段CD上是否存在点T
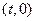，使
，若存在，请说明理由。
相关试题
中，
是
的中点，点
在棱
上运动。
；
所成角为
时，求三棱锥
的体积。
的前项和为
且
满足
且
求数列
满足
的前n项和
中，角
所对的边分别是
,已知
，求
,求
的解集；
的不等式
恒成立，求实数
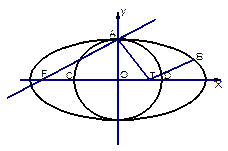
的取值范围．推荐套卷
已知圆o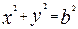：与椭圆有一个公共点A（0，1），F为椭圆的左焦点，直线AF被圆所截得的弦长为1.
（1）求椭圆方程。
（2）圆o与ｘ轴的两个交点为C、D，B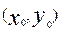是椭圆上异于点A的一个动点，在线段CD上是否存在点T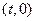，使，若存在，请说明理由。
粤公网安备 44130202000953号