郑已知定点A(0，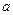
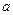)(>0)，直线
：
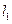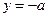交
轴于点B，记过点A且与直线l1相切的圆的圆心为点C．
(I)求动点C的轨迹E的方程；
(Ⅱ)设倾斜角为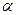
的直线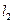
过点A，交轨迹E于两点 P、Q，交直线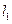于点R．
(1)若tan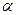=1，且ΔPQB的面积为
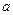，求的值；
(2)若∈[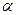
，
]，求|PR|·|QR|的最小值．
在R上是减函数，求实数
的取值范围。
及直线
．
为何值时，直线与椭圆有公共点？
，求直线的方程．
，离心率为0.6，求椭圆的标准方程。
对一切
恒成立, 求
的取值范围。推荐套卷
郑已知定点A(0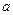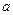，)(>0)，直线 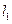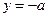：交轴于点B，记过点A且与直线l1相切的圆的圆心为点C．
(I)求动点C的轨迹E的方程；
(Ⅱ)设倾斜角为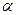的直线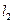过点A，交轨迹E于两点 P、Q，交直线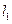于点R．
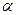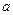(1)若tan=1，且ΔPQB的面积为，求的值；
(2)若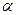∈[，]，求|PR|·|QR|的最小值．
粤公网安备 44130202000953号