(本小题满分12分)
如图，已知三棱柱ABC—A1B1C1的侧棱与底面垂直，AA1＝AB＝AC＝1，AB⊥AC，M、N分别是CC1、BC的中点，点P在A1B1上，且满足＝λ(λ∈R).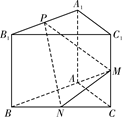
(1)证明：PN⊥AM；
(2
)当λ取何值时，直线PN与平面
ABC所成的角θ最大？并求该最大角的正切值；
(3)若平面PMN与平面ABC所成的二面角为45°，试确定点P的位置
.
是复数，
与
均为实数，且复数
在复平面上对应的点在第一象限，求实数
的取值范围．
=
.
时，求不等式 
的解集包含
，求
的取值范围.
推荐套卷
(本小题满分12分)
如图，已知三棱柱ABC—A1B1C1的侧棱与底面垂直，AA1＝AB＝AC＝1，AB⊥AC，M、N分别是CC1、BC的中点，点P在A1B1上，且满足＝λ(λ∈R).
(1)证明：PN⊥AM；
(2)当λ取何值时，直线PN与平面ABC所成的角θ最大？并求该最大角的正切值；
(3)若平面PMN与平面ABC所成的二面角为45°，试确定点P的位置.
粤公网安备 44130202000953号