.(本小题满分12分)对于函数 ,若
,若 ,则称
,则称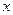 为
为 的“不动点”,若
的“不动点”,若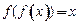 ,则称
,则称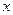 为
为 的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为
的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为 和
和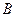 ,即
,即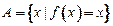 ,
, .
.
(1)求证: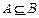 ;
;
(2)若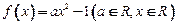 ,且
,且 ,求实数
,求实数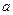 的取值范围;
的取值范围;
(3)若 是
是 上的单调递增函数,
上的单调递增函数,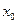 是函数的稳定点,问
是函数的稳定点,问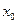 是函数的不动点吗?若是,请证明你的结论;若不是,请说明的理由.
是函数的不动点吗?若是,请证明你的结论;若不是,请说明的理由.
推荐套卷
.(本小题满分12分)对于函数 ,若
,若 ,则称
,则称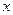 为
为 的“不动点”,若
的“不动点”,若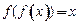 ,则称
,则称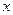 为
为 的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为
的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为 和
和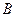 ,即
,即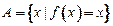 ,
, .
.
(1)求证: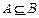 ;
;
(2)若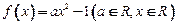 ,且
,且 ,求实数
,求实数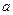 的取值范围;
的取值范围;
(3)若 是
是 上的单调递增函数,
上的单调递增函数,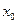 是函数的稳定点,问
是函数的稳定点,问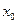 是函数的不动点吗?若是,请证明你的结论;若不是,请说明的理由.
是函数的不动点吗?若是,请证明你的结论;若不是,请说明的理由.