(本题满分 13分)
集合 为集合
为集合 的
的 个不同的子集,对于任意不大于
个不同的子集,对于任意不大于 的正整数
的正整数 满足下列条件:
满足下列条件:
① ,且每一个
,且每一个 至
至 少含有三个元素;
少含有三个元素;
②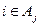 的充要条件是
的充要条件是 (其中
(其中 )。
)。
为了表示这些子集,作 行
行 列的数表(即
列的数表(即 数表),规定第
数表),规定第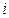 行第
行第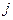 列数为:
列数为: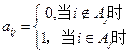 。
。
(1)该表中每一列至少有多少个1;若集合 ,请完成下面
,请完成下面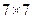 数表(填符合题意的一种即可);
数表(填符合题意的一种即可);
(2)用含 的代数式表示
的代数式表示 数表
数表 中1的个数
中1的个数 ,并证明
,并证明 ;
;
(3)设数列 前
前 项和为
项和为 ,数列
,数列 的通项公式为:
的通项公式为: ,证明不等式:
,证明不等式: 对任何正整数
对任何正整数 都成立。
都成立。
推荐套卷
(本题满分 13分)
集合 为集合
为集合 的
的 个不同的子集,对于任意不大于
个不同的子集,对于任意不大于 的正整数
的正整数 满足下列条件:
满足下列条件:
① ,且每一个
,且每一个 至
至 少含有三个元素;
少含有三个元素;
②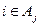 的充要条件是
的充要条件是 (其中
(其中 )。
)。
为了表示这些子集,作 行
行 列的数表(即
列的数表(即 数表),规定第
数表),规定第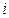 行第
行第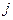 列数为:
列数为: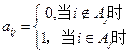 。
。
(1)该表中每一列至少有多少个1;若集合 ,请完成下面
,请完成下面 数表(填符合题意的一种即可);
数表(填符合题意的一种即可);
(2)用含 的代数式表示
的代数式表示 数表
数表 中1的个数
中1的个数 ,并证明
,并证明 ;
;
(3)设数列 前
前 项和为
项和为 ,数列
,数列 的通项公式为:
的通项公式为: ,证明不等式:
,证明不等式: 对任何正整数
对任何正整数 都成立。
都成立。