在如图所示的平面直角坐标系中，△OAB的三个顶点坐标分别为O(0,0)，A(1,-3)，B(3,-2)．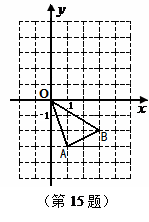
（1）将△OAB绕原点O逆时针旋转90°，画出旋转后的△OA’ B’；
（2）求出点B到点B’ 所走过的路径的长．
相关试题
一次函数
的图象与反比例函数
的图象交于A(1，4)、B(﹣2，m)两点，
（1）求一次函数和反比例函数的关系式；
（2）画出草图，并根据草图直接写出不等式
的解集．
如图，在平面直角坐标系中，抛物线
的顶点A的坐标为（3,15），且过点（－2，10），对称轴AB交
轴于点B，点E是线段AB上一动点，以EB为边在对称轴右侧作矩形EBCD，使得点D恰好落在抛物线上，点D′是点D关于直线EC的轴对称点.
（1）求抛物线的解析式；
（2）若点D′恰好落在
轴上的点（0，6）时，求此时D点的坐标；
（3）直线CD′交对称轴AB于点F,
①当点D′在对称轴AB的左侧时，且△ED′F∽△CDE，求出DE:DC的值；
②连结B D′，是否存在点E，使△E D′B为等腰三角形？若存在，请直接写出BE:BC的值，若不存在请说明理由.
天猫商城旗舰店销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：
，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的60%．
（1）设该旗舰店每月获得利润为w（元），求每月获得利润w（元）与销售单价x（元）之间的函数关系式，并确定自变量x的取值范围．
（2）当销售单价定为多少元时，每月可获得最大利润？每月的最大利润是多少？
（3）如果旗舰店想要每月获得的利润不低于2000元，那么每月的成本最少需要 元？
（成本＝进价×销售量）
相关知识点
推荐套卷
粤公网安备 44130202000953号