如图,在△ABC中,∠C=60°,BC=4,AC=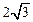 ,点P在BC边上运动,PD∥AB,交AC于D. 设BP的长为x,△APD的面积为y .
,点P在BC边上运动,PD∥AB,交AC于D. 设BP的长为x,△APD的面积为y .
(1)求AD的长(用含x的代数式表示);
(2)求y与x之间的函数关系式,并回答当x取何值时,y的值最大?最大值是多少?
(3)点P是否存在这样的位置,使得△ADP的面积是△ABP面积的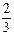 ?若存在,请求出BP的长;若不存在,请说明理由.
?若存在,请求出BP的长;若不存在,请说明理由.
相关知识点
推荐套卷
如图,在△ABC中,∠C=60°,BC=4,AC=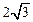 ,点P在BC边上运动,PD∥AB,交AC于D. 设BP的长为x,△APD的面积为y .
,点P在BC边上运动,PD∥AB,交AC于D. 设BP的长为x,△APD的面积为y .
(1)求AD的长(用含x的代数式表示);
(2)求y与x之间的函数关系式,并回答当x取何值时,y的值最大?最大值是多少?
(3)点P是否存在这样的位置,使得△ADP的面积是△ABP面积的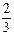 ?若存在,请求出BP的长;若不存在,请说明理由.
?若存在,请求出BP的长;若不存在,请说明理由.