（本小题满分13分）
某班从6名班干部（其中男生4人，女生2人）中选3人参加学校学生会的干部竞选．
（Ⅰ）设所选3人中女生人数为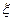
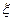，求的分布列及数学期望
；
（Ⅱ）在男生甲被选中的情况下，求女生乙也被选中的概率．
上，求使
取得最大值和最小值的点
的坐标．
是椭圆的两个焦点，
为椭圆上一点，
．
的面积只与椭圆的短轴长有关．
，
，
为双曲线的两个焦点，点
在双曲线上，求
的最小值．
交椭圆
于
两点，且
的距离之和为
，求直线
是椭圆
上的点，求
的取值范围．相关知识点
推荐套卷
（本小题满分13分）
某班从6名班干部（其中男生4人，女生2人）中选3人参加学校学生会的干部竞选．
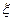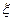（Ⅰ）设所选3人中女生人数为，求的分布列及数学期望；
（Ⅱ）在男生甲被选中的情况下，求女生乙也被选中的概率．
粤公网安备 44130202000953号