已知函数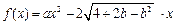 ,
,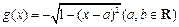 .
.
(1)当 时,若
时,若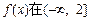 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有整数对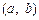 :存在
:存在 ,使得
,使得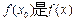 的最大值,
的最大值,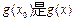 的最小值;
的最小值;
(3)对满足(2)中的条件的整数对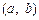 ,试构造一个定义在
,试构造一个定义在 且
且 上的函数
上的函数 :使
:使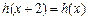 ,且当
,且当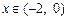 时,
时,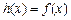 .
.
推荐套卷
已知函数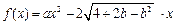 ,
,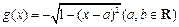 .
.
(1)当 时,若
时,若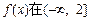 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有整数对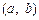 :存在
:存在 ,使得
,使得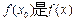 的最大值,
的最大值,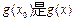 的最小值;
的最小值;
(3)对满足(2)中的条件的整数对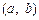 ,试构造一个定义在
,试构造一个定义在 且
且 上的函数
上的函数 :使
:使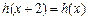 ,且当
,且当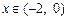 时,
时,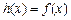 .
.