（本小题满分16分）如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求M在AB的延长线上，N在AD的延长线上，且对角线MN过C点。已知AB=3米，AD=2米。
（I）设
（单位：米），要使花坛AMPN的面积大于32平方米，求
的取值范围；
（II）若
（单位：米），则当AM，AN的长度分别是多少时，花坛AMPN的面积最大？并求出最大面积。
相关试题
为等差数列，且
求
的通项式；
。
，
，
，
，求数列
的前
项和
。
，
，B=450求A、C及c.
．
的图像；
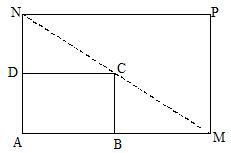
的解集．推荐套卷
（本小题满分16分）如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求M在AB的延长线上，N在AD的延长线上，且对角线MN过C点。已知AB=3米，AD=2米。
（I）设（单位：米），要使花坛AMPN的面积大于32平方米，求的取值范围；
（II）若（单位：米），则当AM，AN的长度分别是多少时，花坛AMPN的面积最大？并求出最大面积。
粤公网安备 44130202000953号